Hendrik Lorentz
18 July 1853 – 4 February 1928
Creator of: Lorentz Transformation
Lorentz transformation
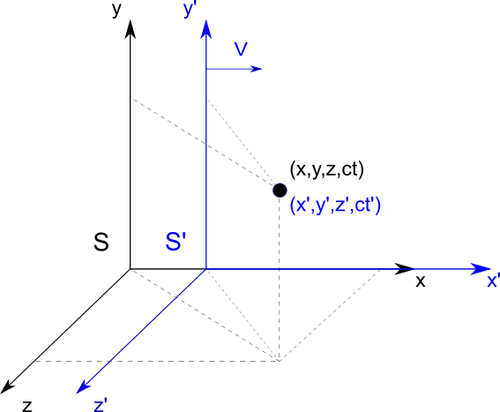
Let's say we have two systems \(S\) and \(S'\). The system \(S'\) is
moving at a speed \(\vec{v}_{x}\) in relation to the system \(S\). Observer in the each
systems is going to define position of the object. From \(S\) perspective object has
position \((x,y,z,ct)\) while from \(S'\) perspective \((x',y',z',ct')\).
To know how the coordinates being transferred between systems we need to find linear transformation because
movement is without acceleration. In this case:
\begin{equation} \label{eq:L1} x' = ax + bt\end{equation}
\begin{equation} \label{eq:L2} x = a'x' + b't'\end{equation}
Where \(a,b,a',b'\) are constants that we need to find.
Beginning of the \(S'(x' = 0)\)
system in \(S\) system is moving with velocity
\(\vec{v}\) then:
$$0 = ax + bt \quad \Rightarrow \quad b = -a\frac{x}{t} = -a\vec{v} $$
Seting this result to the \eqref{eq:L1} equation, and knowing that system
\(S\) is moving from system \(S'\) with velocity \(-\vec{v}\), we get:
\begin{equation} \label{eq:L3} x' = a(x - \vec{v}t)\end{equation}
\begin{equation} \label{eq:L4} x = a'(x' + \vec{v}t')\end{equation}
Both systems are symmetrical, then \(a = a'\)
Let's send both light signal from each system from its beginning
\(x=x'=0\) in the same time \(t=t'=0\). For light speed \(c\) we get:
\begin{equation} \label{eq:L5} x' = ct'\end{equation}
\begin{equation} \label{eq:L6} x = ct\end{equation}
Substituting now equations \eqref{eq:L5} and \eqref{eq:L6} to \eqref{eq:L3} and \eqref{eq:L4}, we get:
\begin{equation} \label{eq:L7} ct' = a(ct - \vec{v}t) \end{equation}
\begin{equation} \label{eq:L8} ct = a(ct' - \vec{v}t') \end{equation}
Multiplying equations \eqref{eq:L7} and \eqref{eq:L8} by parties, we get:
$$c^{2}tt' = a^{2}tt'(c^{2} - v^{2}) $$
$$ \Rightarrow a^{2} =\frac{c^{2}}{c^{2}-v^{2}} $$
\begin{equation} \label{eq:L9} \Rightarrow a = \frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \end{equation}
Now we can write transformation equations for \(x\) and \(x'\)
coordinates:
$$ x' = \frac{x - \vec{v}t}{\sqrt{1-\frac{v^{2}}{c^{2}}}} $$
$$ x = \frac{x' + \vec{v}t'}{\sqrt{1-\frac{v^{2}}{c^{2}}}} $$
To get time transformation we starting from equation \eqref{eq:L4} and
transform to get \(t'\):
$$ t' = \frac{x}{a\vec{v}} - \frac{x'}{\vec{v}} $$
Now we insert value \(x'\) from equation \eqref{eq:L3}:
$$ t' = \frac{x}{a\vec{v}} - \frac{a^{2}(x-\vec{v}t)}{a\vec{v}} $$
$$ \Rightarrow t' = \frac{a^{2}\vec{v}t}{a\vec{v}} + \frac{x(1-a^{2})}{a\vec{v}} $$
Now inserting value \(a\) from equation (9) and after several
transformations we get:
$$ t' = \frac{\vec{v}t + x(1-\frac{v^{2}}{c^{2}}) - x}{\vec{v}\sqrt{1-\frac{v^{2}}{c^{2}}}}$$
$$ \Rightarrow t' = \frac{t - x\frac{\vec{v}}{c^{2}}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$$
Both systems move in relation to the coordinates \(x\), so the
coordinates \(z\) and \(y\) are not transformed. All transformed coordinates are given
below:
\begin{equation} \label{eq:L10} x' = \frac{x - \vec{v}t}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \quad x = \frac{x' + \vec{v}t'}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \end{equation}
$$ y' = y \quad y = y'$$
$$ z' = z \quad z = z' $$
\begin{equation} \label{eq:L11} t' = \frac{t - x\frac{\vec{v}}{c^{2}}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \quad
t = \frac{t' + x'\frac{\vec{v}}{c^{2}}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \end{equation}
Relativistic velocities adding
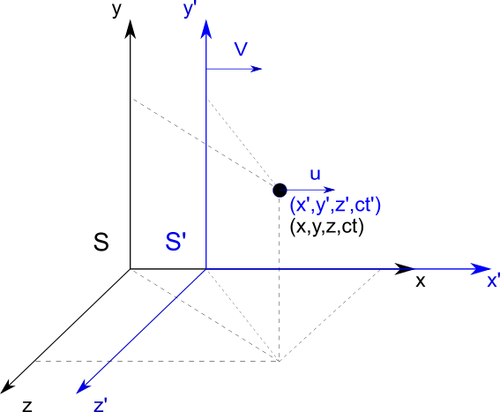
Let say that we observing object that is moving with his own velocity
in another system. We are staying in \(S\) system, the object and his system \(S'\) are
moving away with velocity \(\vec{v}\) from \(S\) system. Object it self is moving with
another velocity \(\vec{u'}\) from \(S'\) system. Using Lorentz transformations \eqref{eq:L10} and \eqref{eq:L11}
we define velocity \(\vec{u'}\) of the moving object in \(S'\) system as:
$$ \vec{u'} = \frac{x'}{t'} = \frac{\frac{x - \vec{v}t}{\sqrt{1-\frac{v^{2}}{c^{2}}}} }{\frac{t -
x\frac{\vec{v}}{c^{2}}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}} = \frac{x - \vec{v}t}{t - x\frac{\vec{v}}{c^{2}}} \quad /t$$
\begin{equation} \label{eq:L12} \Rightarrow \vec{u'} = \frac{\frac{x}{t} - \vec{v}}{1 - \frac{x}{t}\frac{\vec{v}}{c^{2}}} = \frac{\vec{u} - \vec{v}}{1 - \vec{u}\frac{\vec{v}}{c^{2}}} \end{equation}
To get velocity of the object from \(S\) system frame, we need to
transform above equation:
$$ \vec{u} - \vec{v} = \vec{u'}(1 - \vec{u}\frac{\vec{v}}{c^{2}}) $$
$$ \Rightarrow \vec{u}(\vec{u'}\frac{\vec{v}}{c^{2}} + 1) = \vec{u'} + \vec{v}$$
\begin{equation} \label{eq:L13} \vec{u} = \frac{\vec{u'} + \vec{v}}{\vec{u'}\frac{\vec{v}}{c^{2}} + 1} \end{equation}
Velocitis adding example

Two spaceships flying from each other in opposite directions with
the same 0.9 light speed. What is the speed of one spaceship in term of second one.
To calculate this we use \eqref{eq:L12} equation and put \(\vec{v} = 0.9 c\) and \(\vec{u} = -0.9 c\)
( \("-"\) indicates that velocity direction of one spaceship is opposite to the
reference frame).
$$ \Delta \vec{u'} = \frac{\vec{u} - \vec{v}}{1 - \vec{u}\frac{\vec{v}}{c^{2}}} = \frac{-0.9 - 0.9}{1 + 0.9\frac{0.9}{1^{2}}} = \frac{-1.8}{1.81} < |-1|c$$
Second spaceship is moving away from first one with absolute speed
less then speed of light.
Length contraction
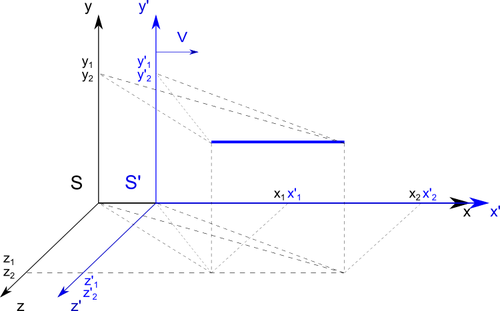
Let say that we observing object that is moving with his own velocity
in another system. We are staying in \(S\) system, the object and his system \(S'\) are
moving away with velocity \(\vec{v}\) from \(S\) system.
The lenght of object in \(S'\)
system is simply calculated by:
$$ L' = x_{2}' - x_{1}'$$
The same object in \(S\) system will by calculated with:
$$ L = x_{2} - x_{1}$$
Where \(x_{1}\) and \(x_{2}\)
are under the influence of Lorentz transformation
thats why we need to use equations \eqref{eq:L10}. Then we get proper length:
$$ L = \frac{x_{2}' + \vec{v}t_{2}'}{\sqrt{1-\frac{v^{2}}{c^{2}}}} - \frac{x_{1}' + \vec{v}t_{1}'}{\sqrt{1-\frac{v^{2}}{c^{2}}}} = \frac{x_{2}' - x_{1}' + \vec{v}t_{2}' - \vec{v}t_{1}'}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$$
Flow of time is the same for all coordinates thats why \(t'_{1} = t'_{2}\).
Simplifying abowe equation we get:
\begin{equation} \label{eq:L14} L = \frac{x_{2}' - x_{1}'}{\sqrt{1-\frac{v^{2}}{c^{2}}}} = \frac{L'}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \end{equation}
Length contraction example

Let say that we staing near railroad tracks and we observing person
in train moving with speed of \(\vec{v}\) = 144 km/h = 40 m/s = 0.04 km/s that holds in his
hands a long stick. Length of the stick is \(L'\) = 10m becose the stic is moving
alongside with \(S'\) train system. To calculate length of stic that we will se, we need
to use equation \eqref{eq:L14}:
$$ L = \frac{10}{\sqrt{1-\frac{0.04^{2}}{300000^{2}}}} = \frac{10}{0.9999999999999911} \approx 10m$$
Like you can se there is fast no lenght difference. To make
this more visible we need to speed up the train. Let them move with speed of
\(V\) = 0.5c, then we get:
$$ L = \frac{10}{\sqrt{1-\frac{0.5^{2}}{1^{2}}}} = \frac{10}{0.8660254037844386} \approx 11.55m$$
Now the length difference is much more visible. Difference will by
about 1.55m.


