Newton equation
Acording to the Newton equation
grawity force is proportional to the ratio of two masses \(mM\) of objects and inversely
proportionally to the square of distance \(r^{2}\) between objects. Constant \(G\) is the
gravity constant first calculated by Cavendish in his
experiment.
$$\vec{F}_{g} = G\frac{mM}{r^{2}}\hat{r}$$
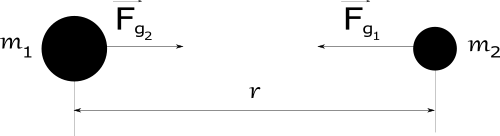
Let we consider two object with masses \(m_{1}\) and \(m_{2}\) on distance
of \(r\) beetwet them. Each of masses prduces attracting force. Mass \(m_{1}\) acts on
mass \(m_{2}\) with force \(\vec{F}_{g_{1}}\) that will pull mass \(m_{2}\) toward mass
\(m_{1}\). On another hand mass \(m_{2}\) acts on mass \(m_{1}\) with force
\(\vec{F}_{g_{2}}\) that will pull mass \(m_{1}\) toward mass \(m_{2}\).
$$\vec{F}_{g_{1}} = G\frac{m_{1}}{r^{2}}\hat{r}$$
$$\vec{F}_{g_{2}} = G\frac{m_{2}}{r^{2}}\hat{r}$$
Combining these two gravitational forces together will create
resultant force equal to:
\begin{equation} \label{eq:C1} \vec{F}_{g_{12}} = G\frac{m_{1}m_{2}}{r^{2}}\hat{r}\end{equation}
Example
Supose we wont to masure gravitational force between Son and Earth.
Considering physical data about those object:
$$m_{1} \sim 1.98 \cdot 10^{30}\mkern3mu [kg]$$
$$m_{2} \sim 5.97 \cdot 10^{24}\mkern3mu [kg]$$
$$r \sim 149.6 \cdot 10^{9}\mkern3mu [m]$$
$$G \sim 6.67 \cdot 10^{-11} \mkern3mu [\frac{m^{3}}{kg \mkern3mu s^{2}}]$$
The pulling force \eqref{eq:C1} will by equal to:
$$\vec{F}_{g_{12}} = 6.67 \cdot 10^{-11} \frac{1.98 \cdot 10^{30} \cdot 5.97 \cdot 10^{24}}{{(149.6 \cdot 10^{9})}^{2}} \sim 3.5 \cdot 10^{22} \mkern3mu [N] $$
This is quite big force.
Newton to Keppler
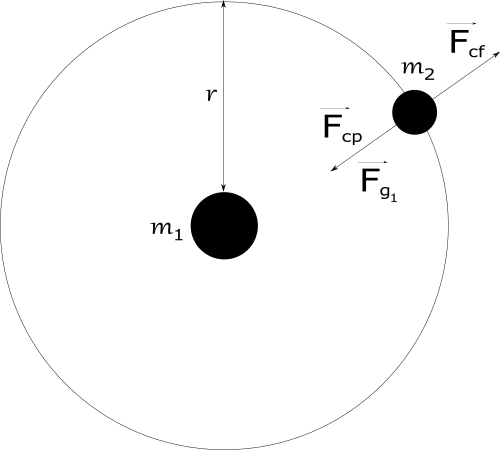
Now question will by why the Moon is not falling on Earth? Falowing
the derivation of Newtons gravitational equation
the centrifugal force is equal to centripetal force.
$$\vec{F}_{cf} = \vec{F}_{cp} = \frac{m_{2}\vec{v}^{2}}{2}\hat{r} $$
Comparing gravitational force \(\vec{F}_{g_{12}}\) that pulls two masses together with
centrifugal force \(\vec{F}_{cf}\) that try to splitt apart this object, we can find the solution thats
holds this system together.
\begin{equation} \label{eq:C2} G\frac{m_{1}m_{2}}{r^{2}}\hat{r} = \frac{m_{2}\vec{v}^{2}}{r}\hat{r}\end{equation}
Linear speed of object on round orbit is equal to:
$$\vec{v} = \frac{2\pi r}{T}\hat{r}$$
Putting velocity to abowe equation and using scalar values we get:
$$G\frac{m_{1}m_{2}}{r^{2}} = \frac{m_{2}4 \pi^{2} r^{2}}{rT^{2}}$$
After reducing and transformation will give us Keppler equation
$$\frac{r^{3}}{T^{2}} = \frac{Gm_{1}}{4\pi^{2}}$$
Linear speed of object can by calculated also from \eqref{eq:C2}:
\begin{equation} \label{eq:C3}\vec{v} = \sqrt{\frac{Gm_{1}}{r}}\hat{r}\end{equation}
Example
Now question will by why the Earth is not falling on Sun?
$$m_{1} \sim 1.98 \cdot 10^{30}\mkern3mu [kg]$$
$$m_{2} \sim 5.97 \cdot 10^{24}\mkern3mu [kg]$$
$$r \sim 149.6 \cdot 10^{9}\mkern3mu [m]$$
$$G \sim 6.67 \cdot 10^{-11} \mkern3mu [\frac{m^{3}}{kg \mkern3mu s^{2}}]$$
The linear speed \eqref{eq:C3} will by equal to:
$$v = \sqrt{\frac{6.67 \cdot 10^{-11} \cdot 1.98 \cdot 10^{30}}{149.6 \cdot 10^{9}}} \sim 29711.8\mkern3mu [\frac{m}{s}] \sim 29.7\mkern3mu [\frac{km}{s}] $$
To balance the gravitational force \(\vec{F}_{g_{12}}\) with centrifugal force \(\vec{F}_{cf}\) Earth need
to by moving on orbit with linear speed of \(29.7\mkern3mu [\frac{km}{s}]\).

